ご訪問ありがとうございます!
解いた数学の問題をマーク方式にして公表するブログです!管理人のRedchopperです!よろしくお願いします!
目次
・今回の問題
・問題の難易度について
・第1問
・第2問
・第3問
・いかがだったでしょうか?〜解いてみた感想〜
今回の問題
八戸工業大学の2020年一般入試の問題です。
この年の問題もマーク方式にして紹介しました。↓
red-red-chopper-mathmatics.hatenablog.com
red-red-chopper-mathmatics.hatenablog.com
問題の難易度について
難易度は☆☆☆です。
昨年よりかは計算量は減りましたが、それでも注意深く計算をしないとミスを誘発してしまいます。解く方針を立てるのは基礎的な知識で充分です。問題文にも要注意です。
難易度表記については以下の記事をご参照ください。
red-red-chopper-mathmatics.hatenablog.com
問題と問題の解説(第1問)
第1問

第1問の解説
問1
ですので、不等式は
と変形できます。この不等式の解はですが、
が問題で要請されていますので
が答えになります。
問2
の2次方程式
を整理すると
となります。この方程式の判別式をとすると
となります。放物線が
軸に接するとき
が条件となりますので、このような
の値は
と
ですが、
が問題文で要請されていますので
が答となります。
問3
与えられている2次関数を式変形(平方完成)すると
となりますので、この関数はのとき最大値
をとります。
問4
求める2次関数をとおくと、点
を通るので
…①
点を通るので
…②
点を通るので
…③
を満たします。①、②、③より、連立方程式
を解くことになりますが、この連立方程式の解はとなりますので、求める2次関数は
となります。
問題と問題の解説(第2問)
第2問

第2問の解説
問1
三角比の相互関係より
となりますので、となります。三角比の相互関係
より
となります。より
ですので
となります。
問2
与えられている条件式の両辺を2乗し、三角比の相互関係を用いての値を求めると
問3
三角形の内角の和がであることより
となります。
に正弦定理を用いると
が成り立ちます。ここからの長さを求めると、
であるので
問4
三角形の3辺の長さが与えられているので、に余弦定理を用いると
問題と問題の解説(第3問)
第3問

第3問の解説
問1
分子と分母をそれぞれ展開します。
よって、与えられた複素数はと変形できます。この複素数の分母を実数化して整理すると
となります。
問2
以下の筆算により、求める余りはとなります。
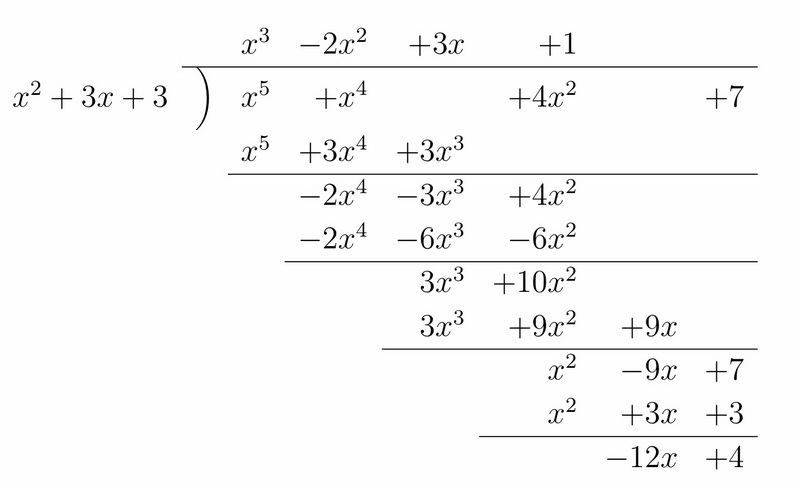
いかがだったでしょうか?〜解いてみた感想〜
去年よりかは計算量が減りましたが、根気強くやっていかないといけないところは変わっていません。
実際の試験時間は60分ですが、問題量としては大問が3つだけなので時間的には余裕はありそうです。
「諦めずに前へ進め」というメッセージが込められているのでしょうか?精神力を鍛えるには良い問題かもしれません。
それでは!またのお越しをお待ちしております!(^^)/
X(Twitter)で更新を報告しています!フォローよろしくお願いします(・ω・)