ご訪問ありがとうございます!
解いた数学の問題をマーク方式にして公表するブログです!管理人のRedchopperです!よろしくお願いします!
今週は代ゼミ高2模試2012年の過去問です。
今回は第2回で出題された図形と方程式の問題です。
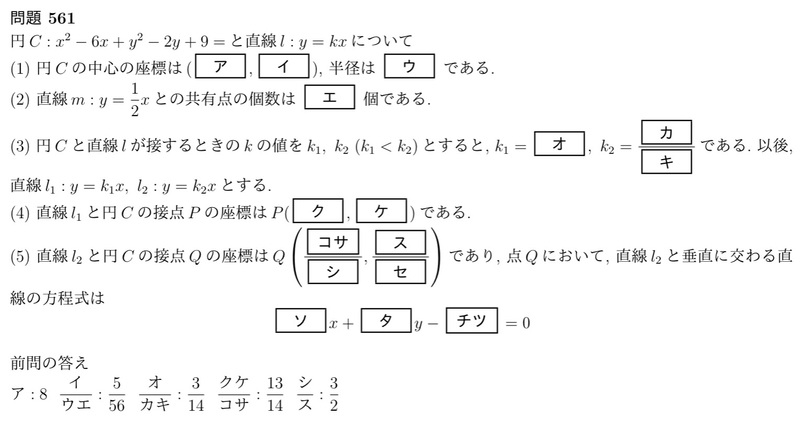
今回の問題について
難易度は☆☆☆です。
図形と方程式の基礎的な問題です。
難易度表記については以下の記事をご参照ください。
red-red-chopper-mathmatics.hatenablog.com
今回の問題の解説
円の方程式はの形に変形すると、円の中心の座標が
、半径が
であることがわかります。
今回の場合ですと、円Cの式はと変形できますので、円Cの中心は
、半径は1であることがわかります。
曲線と直線の共有点の個数は、これらの二つの式の連立方程式の実数解の個数と一致します。
円の方程式はxについて2次式、直線の式はxについて1次式ですので、直線の式を円の式に代入すればxの2次方程式が現れます。
この2次方程式の実数解の個数を調べれば良いのですが、これは2次方程式の判別式によって調べることができます。
この判別式の符号が正なら実数解が2個、0なら1個、負なら無しとなります。
最後の問題は2直線と
が垂直に交わる条件が
であることを使って求めます。
いかがだったでしょうか?
図形と方程式の単元の問題が詰まった問題でした。
おそらく11月ごろに行われたものでしょうか。
復習するには本当に良い問題だと思います。
それでは!またのお越しをお待ちしております!(^^)/
Twitterで更新を報告しています!フォローよろしくお願いします(・ω・)