ご訪問ありがとうございます!
解いた数学の問題をマーク方式にして公表するブログです!
管理人の赤いチョッパーです!よろしくお願いします。
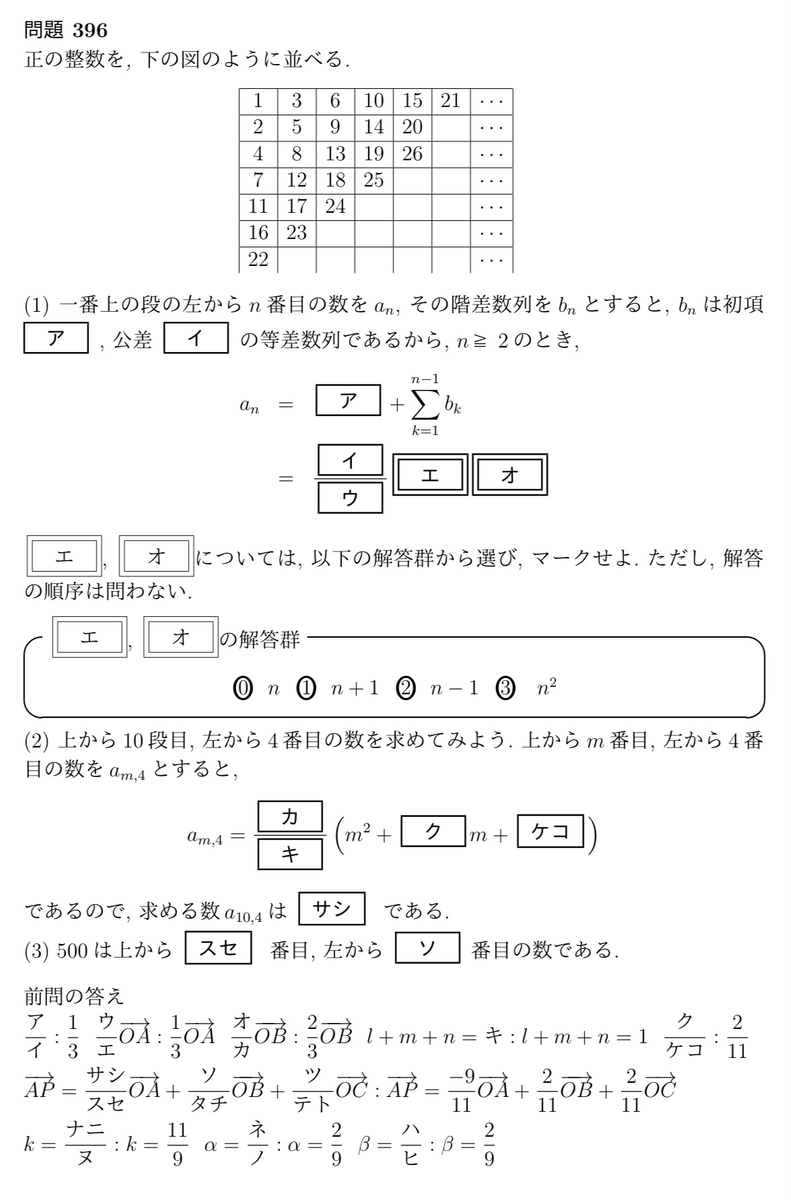
今回は数列を使う問題です。
今回の問題の解説です。
このような問題の解くコツは規則性を見つけることです。
ここでいう規則性とは「n番目をnで表すことができる」ということです。
数が順番に斜めに配置していきますが、横に見るとどうだろうか?縦で見たらどうなるだろうか?と考えていきます。
横で見ると規則性があります。
縦で見ても規則性がありますね。
階差数列をとってみたりしてみてください。
見つけた規則性から問題解決のためのアプローチをかけていきます。
(3)は数を分類していきます。
一番上の段の数に注目します。
一番上の左からn番目の数の次の数は一番左のn+1段目にきます。
その次の数はn段目の左から2番目にきます。
このことを一般化すると、A段目の左からB番目の数でA+B=n+1をみたす数を同じグループに分類します。
A+B=n+1をみたすグループをn番目のグループということにします。
例えば、1は1番目のグループ、18は6番目のグループの数です。
500が何番目のグループの何番目にいるかを探ります。
まずはどのグループに属しているのかを探ります。
このときに一番上の段の数に注目します。
どことどこの間にあるかでどのグループに属しているのかがわかります。
あとは何番目にいるかを探ります。
やり方は群数列のときと同じです。
それでは!またのお越しをお待ちしております!(^^)/