ご訪問ありがとうございます!解いた数学の問題をマーク方式にして公表するブログです!もうすぐ9月が終わりで2021年も終盤戦に入ろうとしています。1年はあっという間ですね…。もうすぐコ◯ナ2周年になっちゃう。早くおわんないかな。そろそろマスク要らずの生活に戻りたいです。
今回に問題は数学Ⅰの教科書の課題学習からです。面白そうなお話があったので問題にしてみました。
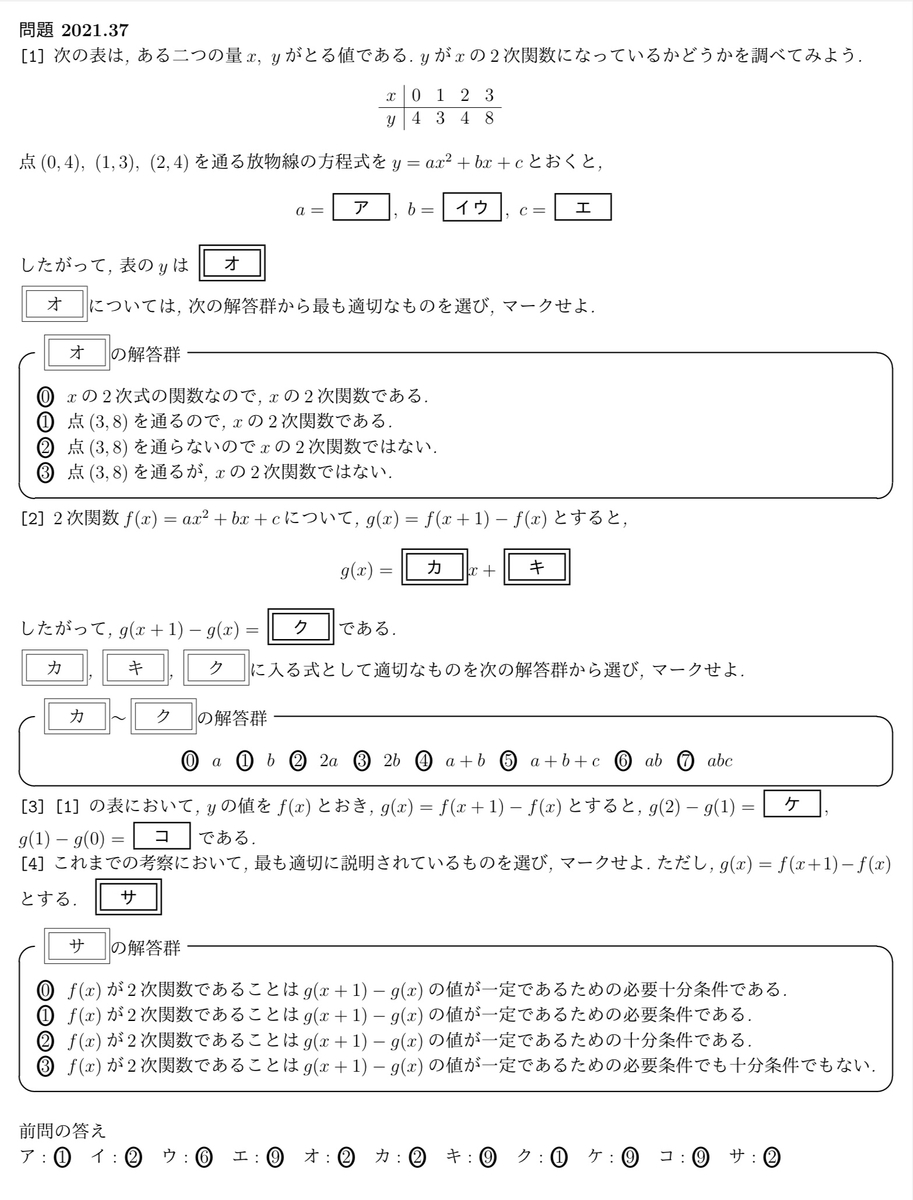
今回の問題で必要な知識
・関数f(x)の扱い
例えば、f(2)ならf(x)の式のxに2を代入します。
・2次関数の決定
通る点を手がかりに連立方程式を立てよう。
課題学習にあった2次関数の性質は、差の差が一定になるということです。やっていることは微分と似ています。この性質を使って、最初にある表が2次関数かどうかを確かめることができます。
しかし、逆はどうでしょうか?つまり、g(x+1)-g(x)が一定ならf(x)は2次関数と言えるでしょうか?g(x+1)-g(x)=0なら、g(x+1)-g(x)は一定です。このとき、g(x)は定数関数と考えられるので、g(x)=cとおきます。したがって、f(x+1)-f(x)=cとなります。f(x)を数列と考えれば、公差cの等差数列と考えられるので、数列の初項をaとすればf(x)=cx+a-cとなります。これは2次関数ではないので、これが反例になります。
教科書には課題学習のような面白そうな話題があるので、良さそうなものがあったら載せていこうと思います。古い教科書も手に入れたので、そこにも面白そうな問題があったら載せていこうかな。昭和の時代は数学Ⅰでベクトルとか式の証明とかやってたんですね。内容が今と比べて倍くらいありました。どんな授業だったのだろうか?
それでは!またのお越しをお待ちしております!(^^)/