ご訪問ありがとうございます!
大学入試は国公立大学の前期日程も終わって、高校入試のほうは公立高校の入試が終わっているところもあればこれからというところもあるようです。もうすぐ数学の問題の速報とか出るかな?入試問題も解いていこうと思っています。
今回は中学以降で習う定理や入試問題で出された定理や面白そうな証明問題をノート形式にしてまとめたものから問題を作ってみました。理解の手助けになればいいかなと思います。
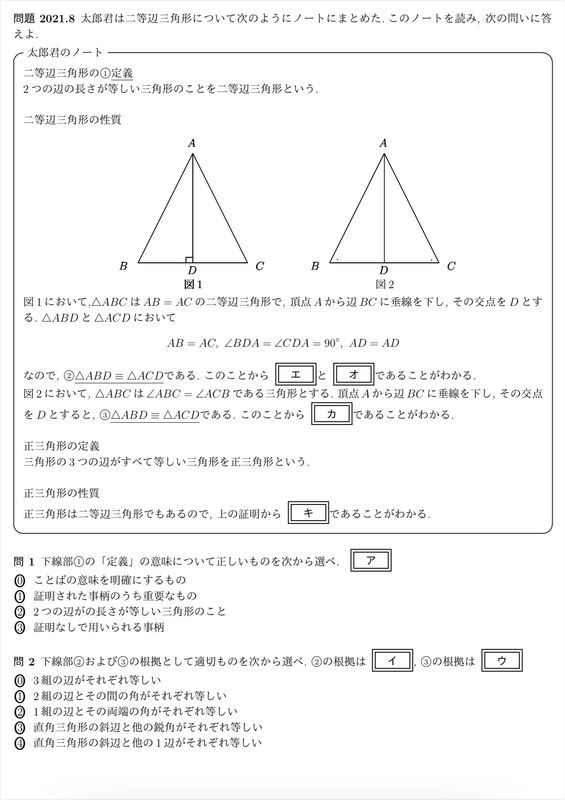

今回は中学2年生で習う二等辺三角形と正三角形の性質からです。合同の証明で初めて証明の問題をやるかと思います。証明が苦手な人が多いようですが、冷静に基本を見つめなおせばできるようになります。数学は「やり方」を覚えれば苦手な人でもできるようになります!(・ω・)
今回の問題を解くための知識を整理しておきます。
・用語の整理
定義:言葉や記号の意味を明確にするもの。
定理:証明された事柄のうち重要なもの。
・証明のやり方
①仮定と結論を確認する。
②仮定や定理を使って結論をいうための根拠を探す
③証明を書く
・三角形の合同条件
①3組の辺がそれぞれ等しい
②2組の辺とその間の角がそれぞれ等しい
③1組の辺とその両端の角がそれぞれ等しい
・直角三角形の合同条件
①直角三角形の斜辺と1つの鋭角がそれぞれ等しい
②直角三角形の斜辺と他の1辺がそれぞれ等しい
今回の太郎君のノートの内容は二等辺三角形で成り立つ定理の証明の概要です。
・二等辺三角形の底辺の垂直二等分線は頂角の二等分線
・二等辺三角形の底角は等しい
この二つの証明が書いてあります。参考書には
・二等辺三角形の頂角の二等分線は底辺の垂直二等分線
であることが書いてあるものが多いかと思います。いずれも三角形の合同を使って証明することができます。証明するときは仮定と結論に気を付けます。「は」で切るとわかりやすいかと思います。上の3つの事柄は日本語で書いてありますが、数式に直すと示すべきことが明確になってわかりやすくなります。根拠も見つけやすくなるのではないでしょうか。
正三角形は3つの辺が等しいですが、「2つの辺が等しい」ともとれるので二等辺三角形の性質が成り立ちます。これを使うと
・正三角形の3つの角の大きさが等しい
・3つの角が等しい三角形は正三角形である
ということがわかります。また、三角形の内角の和は180°なので正三角形の1つの角の大きさは60°であることもわかります。
定理の証明は教科書に書いてあることが多いです。読んだだけではわかりにくいので学校の先生が証明してくれることもあります。大学の講義は本当に重要なものしか証明してくれませんが…。自分でやれってことですかね。理解するのが大変です。高校までで出てくる定理は一度証明しておいたほうが良いです。大学入試で出題されることもありますからね。大阪大学では点と直線との距離の公式の証明、九州大学では和の公式の証明が出題されました。大学のときの指導教官の先生が「公式の証明の出題は学生に対する警告」とおっしゃっていたのを覚えています。自分で教科書をしっかり読むのが大事なんですね。