↑ここで回答した問題です。
円に内接する四角形に関する問題です。

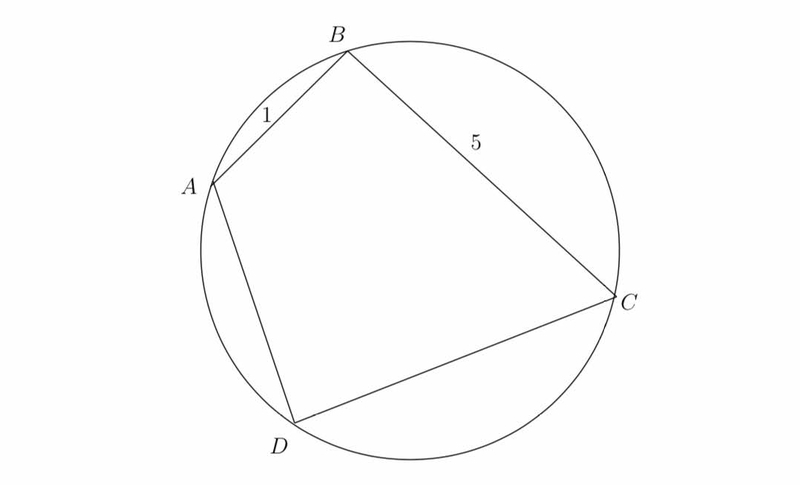
参考図
この質問の意図はこの問題をブラーマグプタの公式を使った解き方を考えられないか、というものでした。
先に回答者がいましたが、「大学入試では証明なしに使えないので、利用しなくてもよい」という意図外れの解答でした。
質問者が受験生なら答える気はなかったのですが、趣味で数学をしているそうなので、同じ立場なら考えてみようかということで考えてみました。
実はこの質問を見てブラーマグプタの公式を初めて知りました。
大学院にまで行って数学をしたのに…。
それだけ使わない公式ということなんでしょうね。
ヘロンの公式でさえあまり使わないのに。
ブラーマグプタの公式はこれです。

第一印象は「ヘロンの公式っぽい」でした。
問題で面積が与えられているので使えるんじゃないかと思いました。
どうやって使うかがあまり見えてこない…。
そういう時はとりあえず考えられる方法で解く!
ということで、一度解いてみました。

これが普通の解き方かと思います。
質問者さんも一度この方法で解いていらっしゃってたようです。
問題はブラーマグプタの公式が使えるかどうかです。
公式に当てはめようとすると、円に内接する四角形の4つの辺の長さの情報が必要になります。
そこは最初に解いた方法で情報が出ています。
(4)がその情報です。これでsの値は出そうです。
ブラーマグプタの公式を使う準備ができました。やってみましょう。

(5)からCDとADの値をどうやって絞り込むかです。
考えられる候補は次のようになるかと思います。
・7-AD=8と7-CD=1
・7-AD=4と7-CD=2
(4)を考慮すれば後者が適しています。
しかし、ここで一つ疑問が残ります。
それは「ADとCDは整数かどうか」です。
問題文をよく読んでみると「CD>AD」以外条件がありません。
つまり、ADとCDの値が整数である保証がありません。
整数じゃない値があったらどうするんだ?っていう話です。
最初に解いた方法は最後に解と係数の関係を使ってADとCDの値を導き出しました。
これは実数全体から候補を一意に絞り込みました。
一方、ブラーマグプタの公式を使う方法はADとCDの値は整数全体から候補を絞りました。
別の解き方でADとCDの値が整数であることがわかっているのですが、わかってないこと前提で解くとこの方法は良いとは言えないです。
整数以外の解がないということはブラーマグプタの公式を使う解き方では言っていませんからね。
ここまでの考察で
・ブラーマグプタの公式を使うことはできる
・ブラーマグプタの公式を使った場合、ADとCDの値の絞り込みは整数であること前提になる
・そうなると「ADとCDが整数ではない」ことを否定する説明ができない
ということであると考えました。
そういう理由で質問者さんには「ブラーマグプタの公式を使うことは適当ではない」という回答を出しました。