マーク方式の数学の問題を作ってみた。

仕事や趣味で数学の問題を解いています。その解いた問題や他に作った問題をマーク方式の問題にして出題しながら日常をつぶやきます。

円周率が３だと証明した⁉Yahoo!知恵袋に現れた主張の矛盾を暴く！

日記入試問題を使ってみた

ご訪問ありがとうございます！

解いた数学の問題をマーク方式にして公表するブログです！管理人のRedchopperです！よろしくお願いします！

今回は問題ではなく、気になったことがありましたのでそれを書いていこうと思います。

2016年頃に「円周率は3であることを証明した」と主張する人物が現れました。

誰が見ても嘘か間違っていることはわかるだろうと思います。

だって、円周率が3であることが正しいかったらずっと3で計算しているはずですもんね！そのほうが計算も楽ですし。

でも、小学校では $3.14$ 、中学以降では $\pi$ が使われていて、大学以上で行われる数学の研究でも円周率 $\pi$ は大活躍です。

では、なぜ円周率は３ではなくて $3.14\cdots \cdots$ や $\pi$ が使われているのでしょうか？

このような観点から入試問題を使って「円周率が３である」と主張している人物の矛盾を暴いていこうと思います！

円周率を3であることを証明した人物

Yahoo!知恵袋に突如現れ、「円周率が３であることを証明した」と主張する人物は、調べによると「植野和男」という人物です。

詳細のプロフィールはこちらです。↓

chiebukuro.yahoo.co.jp

自己紹介によると「元東京都公立中学校教員で、退職後仙台市で年金暮らし。１１年前から円周率π＝３の証明が出来たけど。　ベクトルの大きさを理解出来ない人が多いので、世界に発表する事が出来ない。円周は点ベクトルの集合体だから、線分では表せない。ベクトルは長さで表せない、力と同じで大きさで表示できる量です。3.14は誤りです。」とのことです。（2016年に書いたものと思われます）

しかし、彼の $\pi =3$ の証明がどこにも見つかりませんし、質問の回答も矛盾している点が多く見受けられます。

自己紹介の文章にも不可解な点がありますね。

「位置ベクトル」ならわかりますが「点ベクトル」とは何でしょう？

「ベクトルは長さでは表せない」とおっしゃっていますが有向線分の大きさは何を表しているのでしょうか？

理科の教員だったそうですが、まともに数学と物理学の勉強を行っていたのかが疑問です。

円周率が3であることが正しいというのであれば「世界に発表することができない」理由を「ベクトルの大きさ」の定義とともに明示いただいて証明をしてほしいと思います。

ですが、彼の主張を覆す資料のほうが多く見受けられました。

その一つが2003年、東京大学で出題されたとある問題です。

今回の問題について～なぜ円周率は3ではなく $3.14$ や $\pi$ を使うのか～

東京大学2003年の理系の問題で次のような問題が出題されました。

「円周率が $3.05$ より大きいことを証明せよ」

入試数学では超有名な問題で、知らない人は少ないかと思います。伝説の問題としても扱われてるみたいですね。

円周率は $\displaystyle \frac{円周}{直径}$ で定義されています。

今はこの値をわからないものとして扱いますので $X$ とおきます。

この定義から、半径1の円の円周の長さは $2X$ となります。

この $X$ の値を求める方法の一つとして円に内接する正多角形の周の長さと比較する方法があります。

ここで注意したいのは、 $\sqrt{2}$ や $\sqrt{3}$ のような2乗根の近似値はわかっているものとして扱います。

円とその円に内接する正六角形について考えてみます。図で表すとしたのようになり、赤色が円周、青色が円に内接する正六角形です。

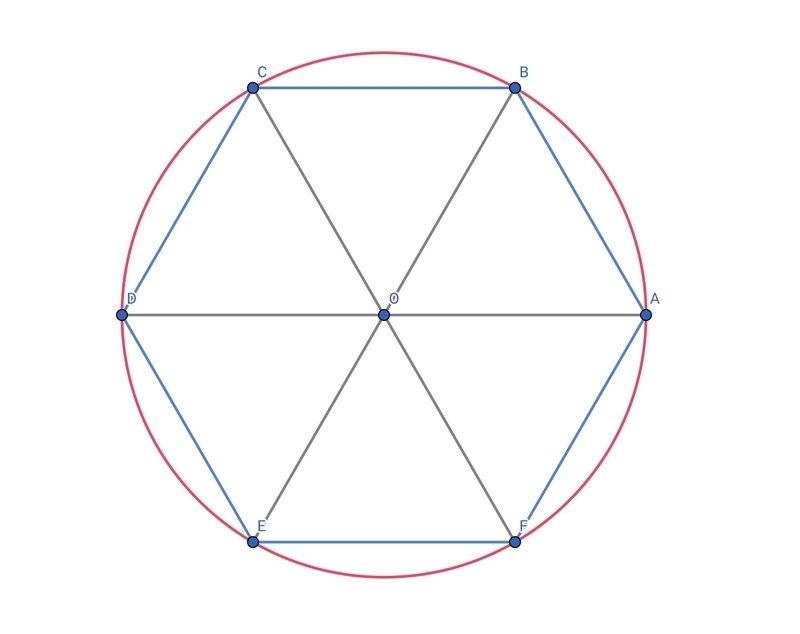
円に内接する正六角形の1辺の長さを求めてみます。

図では円の中心に向かって補助線を引いていますが、このできた三角形に対して余弦定理を使います。

$\triangle AOB$ に注目して考えてみます。

円の半径は1と設定していますので、 $AO=BO=1$ です。

また、中心は6等分していますので、 $\angle AOB=60^{\circ }$ となっています。

したがって、 $\displaystyle AB^{2}=1+1-2\cos{60^{\circ }}=1$ ですので $AB=1$ です。

したがって、正六角形の周の長さは6となります。

2点間の距離は線分が最短ですので $2X＞6$ すなわち $X＞3$ という結果が出てきます。

この結果から円周率は3より大きいことが言えます。つまり、円周率は3ではないということですね。

円周率が3だと主張するのであれば、上の図の赤い線で描いた円と青い線で描いた正六角形がピッタリ重なるはずですが、明らかにそうではないです。

仮に正しいとすれば、円周が折れ線となりますので「円周は線分で表すことができない」と矛盾します。

円と正十二角形で考えるとどうなるでしょうか？図で表してみると以下のようになります。

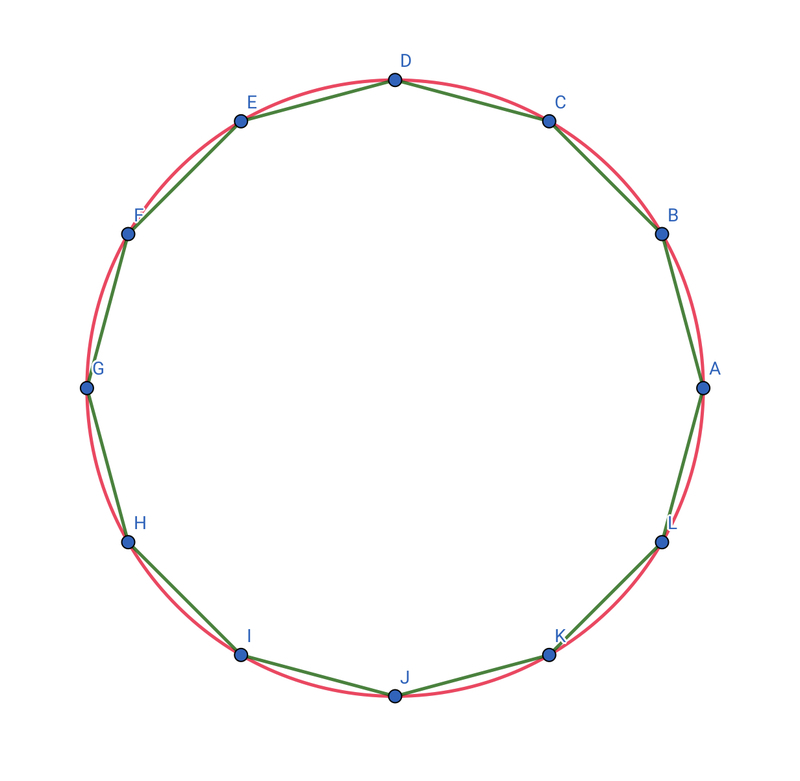
緑色の線が円に内接する正十二角形です。

先ほどと同じように正十二角形の周の長さを求めてみます。

図には書いていませんが、円の中心を $O$ とし、 $\triangle AOB$ について余弦定理を用いります。

$\angle AOB=30^{\circ }$ ですので、 $AB^{2}=1+1-2\cos{30^{\circ }}=2-\sqrt{3}$ となります。

したがって、 $\displaystyle AB=\sqrt{2-\sqrt{3}}=\frac{\sqrt{6}-\sqrt{2}}{2}$ となりますので、正十二角形の周の長さは $6(\sqrt{6}-\sqrt{2})$ となります。

2点間の距離は線分が最小となりますから、 $2X＞6(\sqrt{6}-\sqrt{2})$ すなわち $X>3(\sqrt{6}-\sqrt{2})$ ということになります。

ここで $\sqrt{2}=1.414,\ \sqrt{6}=2.449$ とすると $\sqrt{6}-\sqrt{2}=1.035$ となりますので、 $X＞3.105(＞3.05)$ ということになります。

これで問題が解けたのと同時に $X$ がよく知られている円周率の値に近づいていそうであることがわかったかと思います。

さらに、半径1に外接する正多角形を考えると、円に外接する正六角形の場合は周の長さが $4\sqrt{3}$ になりますので $3＜X＜2\sqrt{3}=3.464$ 、円い外接する正十二角形の場合は周の長さが $24(2-\sqrt{3})$ となりますので $3.105＜X＜3.216$ ということが言えます。

視覚的に見ると、辺の数を増やすほど円に外接する正多角形の辺と円に内接する多角形の辺は同じ円周に近づいていきますので、 $X$ の値はある値に近づきそうな感じがします。

この値が無理数だと知られていますので $\pi$ とおいていると言えそうです。

いかがだったでしょうか？

入試問題は受験生の公平性を担保するために正しい問題を出題することは当然のことですので、問題自体に間違いが無いと思っていても良いかと思います。

勉強、特に数学を勉強することは発信された情報の真偽を確かめるために役に立つツールであると言えるのではないでしょうか。

主張されていることがおかしいと思ったら確かめて裏をとることが非常に大事ですね。

　

それでは！またのお越しをお待ちしております！(^^)/

Twitterで更新を報告しています！フォローよろしくお願いします(・ω・)

https://twitter.com/red_red_chopper