2022年共通テスト本試験数学Ⅰ・数学Aの問題 - マーク方式の数学の問題を作ってみた。

ご訪問ありがとうございます！解いた数学の問題をマーク方式にして公表するブログです！管理人の赤いチョッパーです。よろしくお願いします。

今回は先週の共通テストで出題された数学①の数学Ⅰ・数学Aの問題を解いてみましたので、解説をしていこうと思います。

終了後になんか、ザワザワしていましたね。大手予備校の予想平均点が40点下回っていてセンター試験を合わせても過去最低だと聞きました。他から聞くところによるとセンター試験になる前の共通1次試験を合わせても過去最低だとか。水曜日あたりに大学入試センターから中間集計が発表されました。その集計によると数学Ⅰ・数学Aの平均点は40点を若干上回っていました。それでも平均点は去年から落ちています。難化したと聞きますがどうなのでしょうか？その辺りも考察しながら問題を解説していきたいと思います。

f:id:red-red-chopper:20220122080746j:plain

表紙です。アイキャッチ画像用です。「不正行為には厳正に対処します。」と書かれていますが、そういえば去年の共通テストでは逮捕者が出たようですね。マスクしない男(40代)10代の受験生たちはキチンとしているのに情けない。今年は不正行為以上のことが起こりました。意識不明だった72歳の男性は危機を脱したそうです。

それでは、本題に入っていこうと思います。次の画像からは問題です。

問題の解説

f:id:red-red-chopper:20220122080959j:plain

3文字の対称式の問題です。すべての対称式は基本対称式で表すことができることが知られていますが、3文字の場合の基本対称式は $a+b+c,\ ab+bc+ca,\ abc$ の3つがあります。これらで表すことができないかを考えてみます。

今、 $a+b+c=1,\ a^{2}+b^{2}+c^{2}=13$ という条件が与えられています。 $(a+b+c)^{2}$ を展開すると

$(a+b+c)^{2}=a^{2}+b^{2}+c^{2}+(ab+bc+ca)$

になりますので、条件式の①と②を使うと $ab+bc+ca=-6$ であることがわかります。また、

$(a-b)^{2}+(b-c)^{2}+(c-a)^{2}=2(a^{2}+b^{2}+c^{2})-2(ab+bc+ca)$

ですので、ここまで分かったことを用いると「ウエ」は「38」となります。

f:id:red-red-chopper:20220122081003j:plain

後半は前半で分かったことを使います。xとyの置き方から、x+yはcが上手く消えるので $x+y=-(a-b)$ になります。したがって、 $x+y=-2\sqrt{5}$ となります。(1)の計算から

$(a-b)^{2}+x^{2}+y^{2}=38$

でしたので、 $a-b$ の値を代入すると $x^{2}+y^{2}=18$ となります。

$x+y$ と $x^{2}+y^{2}$ の値がわかったので、この2式から $xy$ の値を求めます。

$(x+y)^{2}=x^{2}+y^{2}+2xy$

この式から $xy$ の値を求めると、 $xy=1$ であることがわかりますので

$(a-b)(b-c)(c-a)=(a-b)xy=2\sqrt{5}$

となります。これで第1問の前半は終了です。

f:id:red-red-chopper:20220122081007j:plain

第1問の後半は図形と計量の問題になります。その前半は三角比の表を使った問題です。図1の $\theta$ が16°なので、縮尺が図の通りであれば三角比の表より $\tan{\theta}=0.2867$ になります。三角比の定義に従うと $\displaystyle \frac{BC}{AC}=0.2867$ となります。ところが、図1の縮尺は水平方向が $\displaystyle \frac{1}{100000}$ 、鉛直方向が $\displaystyle \frac{1}{25000}$ ですので、実際の $\tan{\theta}$ の値は実寸に直して考えると

$\displaystyle \tan{\theta}=\frac{BC\times 25000}{AC\times 100000}=\frac{BC}{4AC}=0.0716$

となりますので、「コ.サシス」には「0.072」が入り、実際の $\tan{\theta}$ の値はtan4°とtan5°の間にあるので $\theta$ の値は4°より大きく5°より小さくなります。

f:id:red-red-chopper:20220122081019j:plain

図形と計量の問題の後半は正弦定理を使う問題でした。条件は $\triangle ABC$ の外接円の半径が3であることです。外接円の半径を使うといえば正弦定理です。

(1)図が描いてませんので、まずは問題文を読んで図を描きます。 $AB=5,\ AC=4$ のとき、正弦定理より

$\displaystyle \frac{4}{\sin{\angle ABC}}=6$

ですので、 $\displaystyle \sin{\angle ABC}=\frac{2}{3}$ となります。また、三角比の定義に従うと

$\displaystyle AD=AB\sin{\angle ABC}=\frac{10}{3}$

となります。

(2)正弦定理を使ってABのとりうる値の範囲を求めます。ABとACに関する条件から

$AC=14-2AB$

となります。正弦定理より

$\displaystyle \frac{AC}{\sin{\angle ABC}}=6$

と $0°\leqq \angle ABC \leqq 180°$ から $4\leqq AB<7$ が出てきます。記述ならここで終わってしまいそうな気がします。しかし、問題文と解答欄が合いませんのでまだ何かがあります。もう一度正弦定理を使って別の式を出してみると

$\displaystyle \frac{AB}{\sin{\angle ACB}}=6$ …(※)

が出てきます。この式と $0°\leqq \angle ACB\leqq 180°$ であることからAB≦6が出てきます。ここまでで正弦定理を2回使いましたが、両方とも満たさなければなりませんので、ABのとりうる値の範囲は $4\leqq AB\leqq 6$ ということになります。

式(※)より

$\displaystyle AD=AB\sin{\angle ABC}=\frac{AB\times AC}{6}$

になりますので、最初のABとACに関する条件から

$\displaystyle AD=-\frac{1}{3}AB^{2}+\frac{7}{3}AB$

になります。ABに関する2次関数なので、平方完成をして最大値を取るようなABの長さを求めれば良いです。答えはAB=4のとき最大値は4です。 f:id:red-red-chopper:20220122081023j:plain

第2問の前半は2次方程式と2次関数の問題です。(1)は具体的にpとqの値が与えられているので、判別式をとって2つの方程式の実数解の個数を調べます。ここで注意するべきことは2つの方程式に共通解があるかどうかです。(1)の最後の問題でここに気がつくかどうかがカギになります。したがって、(2)でn=3となるパターンは

1. 二つの方程式がともに異なる二つの実数解を持ち、共通解が一つ存在する

2. 二つの方程式のうち一方が異なる二つの実数解を持ち、他方が重解を持ち、さらに共通解が存在しない

が考えられます。

f:id:red-red-chopper:20220122081027j:plain

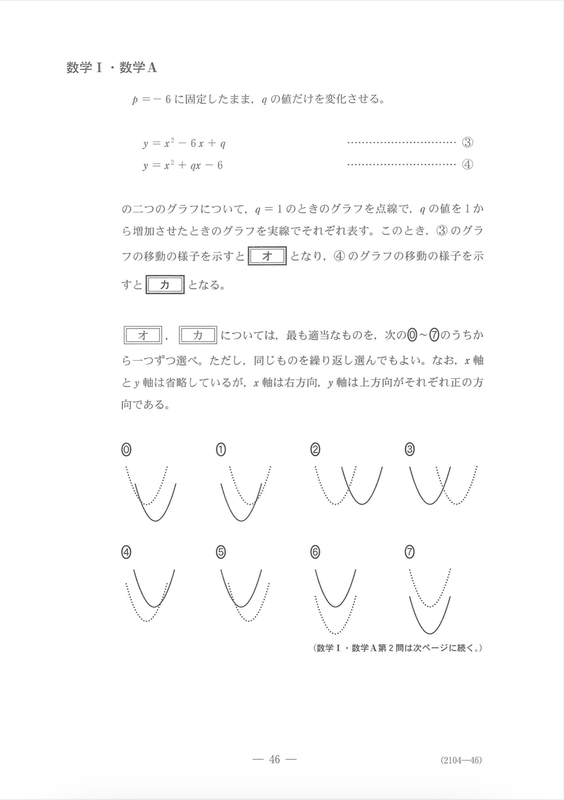
f:id:red-red-chopper:20220122081031j:plain

ここは平方完成させて考えます。

③のグラフは $y=(x-3)^{2}+q-9$

④のグラフは $\displaystyle y=(x+\frac{q}{2})^{2}-\frac{q^{2}}{4}-6$

となりますので、③のグラフでqの値を増加させるとグラフは上へ平行移動し、④のグラフはqの値を増加させると左下へ平行移動します。

f:id:red-red-chopper:20220122081035j:plain

ここは不等式に文字が入っているので少し難しかったかもしれません。具体的にqに整数値を与えて考えるといいかもしれません。集合Aと集合Bには包含関係が無いので、「キ」には③が入ります。一方、 $B\subset \bar{A}$ が成り立つので、「ク」には①が入ります。

f:id:red-red-chopper:20220122081040j:plain

f:id:red-red-chopper:20220122081044j:plain

f:id:red-red-chopper:20220122081048j:plain

f:id:red-red-chopper:20220122081053j:plain

f:id:red-red-chopper:20220122081057j:plain

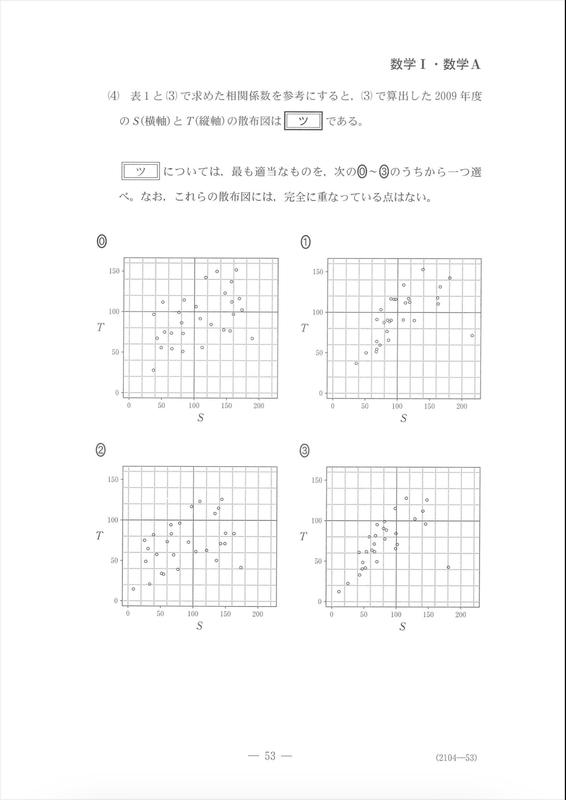
f:id:red-red-chopper:20220122081102j:plain

第2問の後半はデータの分析からの問題です。四分位数、中央値や最大値と最小値に注目して読み取れば、正しい図が選べるかと思います。最後の散布図は相関係数から2つが消えます。残りは平均値から正しい散布図を選びます。「ツ」は③が正解です。

f:id:red-red-chopper:20220122081105j:plain

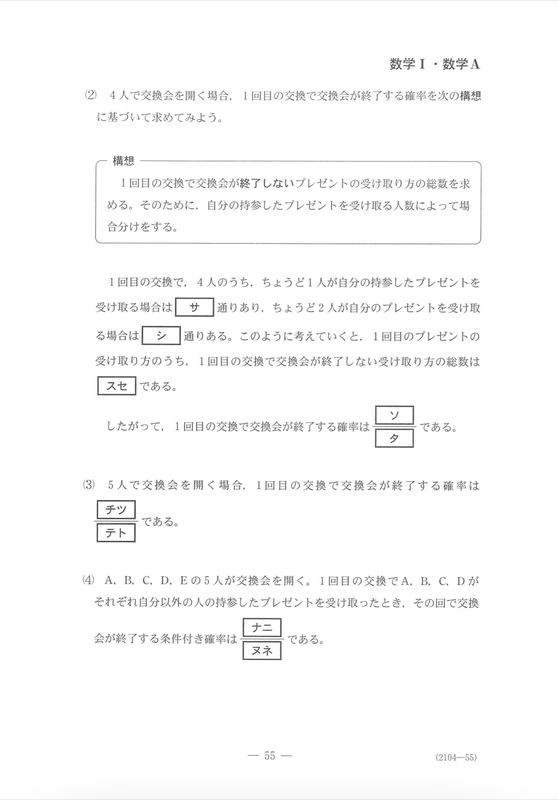
f:id:red-red-chopper:20220122081109j:plain

第3問は確率の問題です。確率の問題は試行のルールを理解することから始めます。この問題の場合はプレゼントを交換して全員が自分以外のプレゼントを受け取ったら交換終了です。1回で交換が終了する確率を求めてみよう、というのがこの問題です。

この問題には「完全順列」という近道がありました。このブログ内でも出題しました。

red-red-chopper-mathmatics.hatenablog.com

参加者とその参加者が持ち寄ったプレゼントを番号で紐付けして考えます。1番の人が持ってきたプレゼントを「1」とします。参加者に1列に並んでもらってランダムにプレゼントを渡します。このとき、どのk番の人がプレゼント「k」を受け取っていないようなプレゼントの並び方が何通りあるかを数えます。2人の時は1通りあるので、2人でプレゼント交換をして1回で終了する確率は $\displaystyle \frac{1}{2}$ となります。3人のときはプレゼント交換が終了する配り方(完全順列)が2通りあって、すべての配り方が3！=6通りあるので、3人でプレゼント交換をして1回で終了する確率は $\displaystyle \frac{1}{3}$ となります。なお、プレゼント交換が終了しない確率はこの余事象になります。(2)以降は完全順列を知らない人向けの解き方が誘導されています。(1)で数え上げたものがヒントになっています。(3)は(2)で数えた方法を行えば、確率を求めることができます。(4)の条件付き確率は、A,B,C,D,E全員が自分以外のプレゼントを受け取る場合の数とEだけが自分のプレゼントを受け取る場合の数を数え上げます。これらの場合がA,B,C,Dがそれぞれ自分以外のプレゼントを受け取る場合です。このうち交換が終了する場合の数も求めていますので、ここの条件付き確率は

(A,B,C,D,E全員が自分以外のプレゼントを受け取る場合の数)÷(A,B,C,Dがそれぞれ自分以外のプレゼントを受け取る場合の数)

で求めることができます。

f:id:red-red-chopper:20220122081112j:plain

f:id:red-red-chopper:20220122081116j:plain

第4問は整数の性質からの問題です。(4)で $11^{5}$ が出てきて戸惑うかもしれませんが、(3)までで解いたことに倣って解いていけばそこまで難しくは無いです。が、計算が非常に大変です。

問題文に沿って進めていきます。625を16で割ったあまりは問題文の通り1です。これを式で表すと

$625=16\times 39+1$

となることがわかります。したがって、①の不定方程式の整数解を求めると、kを整数とすると

$625(x-1)=16(y-39)$

625と16は互いに素なので

$x-1=16k,\ y-39=625k$

を満たすxとyが一般解です。この解からxが2桁の正の数で最小のものを探せば良いことになります。(2)の考察において、 $625^{2}=5^{8}$ であることと $625=2^{4}m+1$ とおくと

$625^{2}=2^{8}m^{2}+2^{5}m+1=2^{5}(2^{3}m^{2}+m)+1$

であることに注目すれば、 $625^{2}$ は $5^{5}$ で割り切れ、 $2^{5}$ で割ると1余ることがわかります。

不定方程式②の解ですが、 $5^{5}x$ を $2^{5}$ で割ると1余ることから、 $5^{5}x-625^{2}$ は $2^{5}\times 5^{5}$ で割り切れます。そこで、lを整数とすると

$5^{5}x-625^{2}=5^{5}\times 2^{5}l$

したがって $5^{5}x=5^{5}\times 2^{5}l+625^{2}$ となりますが、この両辺を $5^{5}$ で割ると $x=32l+125$ となります。このうちxが3桁の正の整数で最小のものをここから探しますと、l=0のときが該当しますので、そのときのxの値とyの値を計算して求めます。

ここまででやってきた解き方と全く同じように(4)の不定方程式を解きます。この解法ではx=19まではなんとか求められますが、yの値を求めることがとても大変です。何かいい方法はないかなぁ？

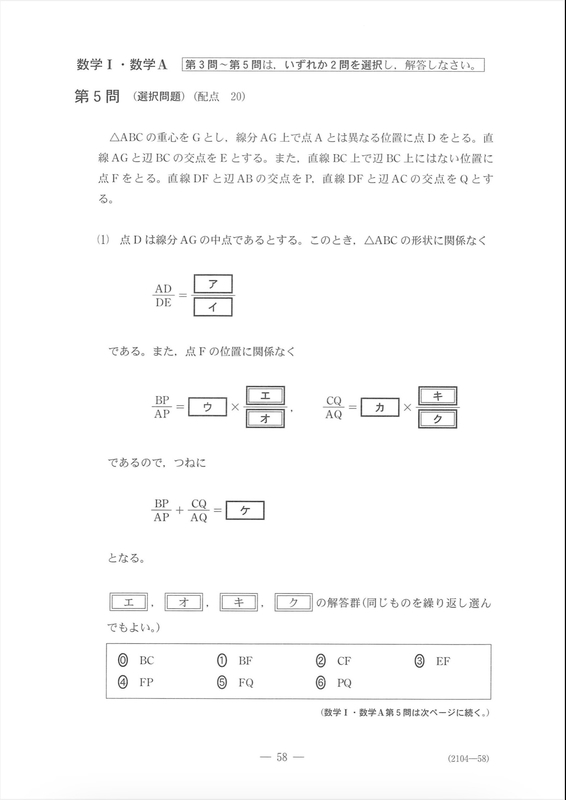
f:id:red-red-chopper:20220122081121j:plain

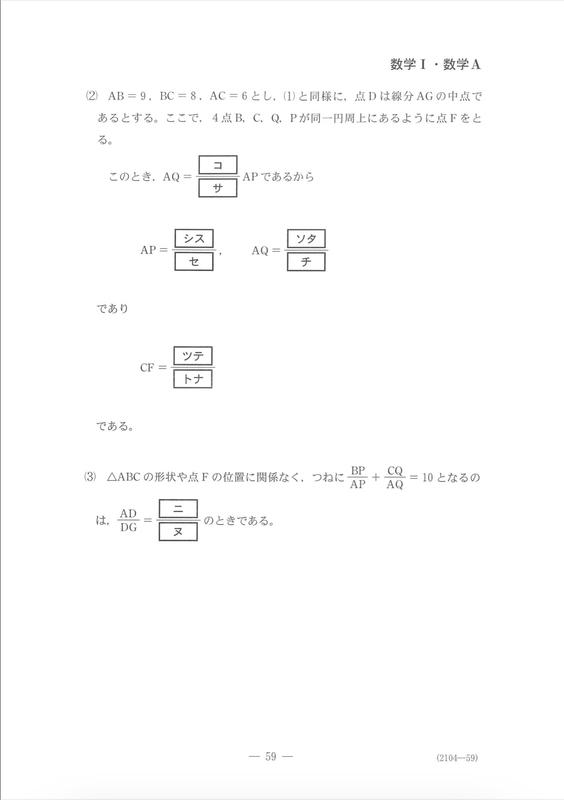
f:id:red-red-chopper:20220122081125j:plain

第5問は図形の性質からの問題です。この問題は他の問題と比べれば非常に簡単でした。メネラウスの定理を繰り返し使えば(2)までは行き着くかと思います。最後の(3)の問題は $\displaystyle \frac{AD}{DE}=k$ とおいて、(1)と同じことをやれば条件式からkの値が求められますので、そこからADとAGの長さをAEで表してADとDGの比を求めればクリアです。

解いてみた感想

問題自体はめちゃくちゃ難しいというほどではなかったです。ただ、全体的に計算量が多く、計算ミスをしてしまったら取り返しのつかないレベルで時間が厳しいと感じました。また、導入文も不要な部分が多く、真面目に読んでいた受験生の方にとっては全く時間が無い厳しいテストではなかったのではないでしょうか。

見えてきた共通テストの傾向

特に第3問以降の数学Aの分野での問題に多かったですが、初めに易しめの問題(今回は易しいと言い難いですが)で問題の導入と解き方の誘導がありました。最後の問題で難しめの問題を設定していますが、導入部分で行ったことと同じようにやっていけば解ける問題ではありました。どこかの問題集に「(1)は(2)のヒント、(1)、(2)は(3)のヒント」と書いてありましたが、そのような傾向が強い問題だったと感じました。

それでは！またのお越しをお待ちしております♪(^^)/