三角比の問題ver20180525

 

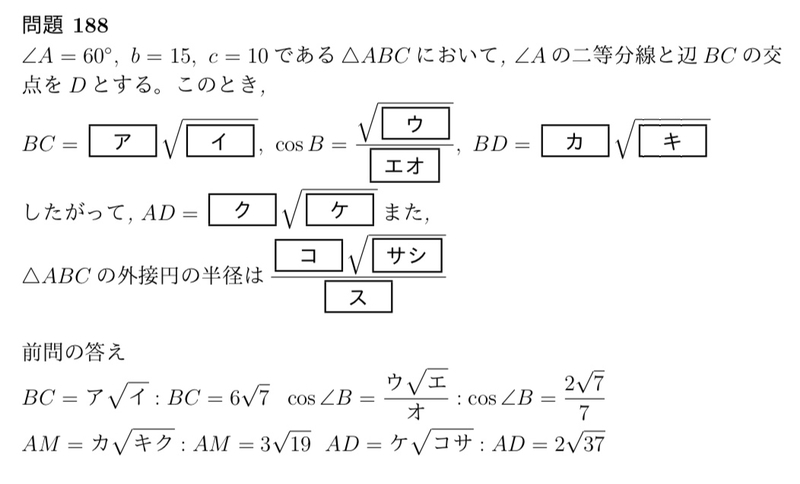
今日も青チャートからの問題です。

基本問題なので簡単かもしれません。

どういう時にどの定理を使えばいいかは、定理の主張と証明を見ればわかります。

 

まずは正弦定理です。

証明の方針は「今まで習ったものを使えないか」を考えます。

あとは定理の主張を確認します。

外接円の半径が関係しているので、外接円の半径を使うように証明できないかを考えます。

でも、初見だとほぼ無理かもしれませんね。

そういうときは教科書や専門書などを参考にして方針を覚えます。

正弦定理の証明の方針は直角三角形を作って辺の長さを表すことができないかを考えます。

三角比の定義を使うには直角三角形が要りますからね。

円周角の定理から同じ弧に対する円周角は一定なのでこれを使えば証明出来そうです。

正弦定理の等式を見ると、1組の角とその対辺の値から直径の長さが分かります。

なので、使うときは1組の角とその対辺ともう一つの要素(角か辺の長さ)が分かれば使うことができます。

この問題の場合は最後に外接円の半径を求める時に使いますね。

次に余弦定理です。

余弦定理の証明の方針も直角三角形を使えないか考えます。

元をたどると三角比の定義に戻りますが、ここで直角三角形が必要です。

最後は三平方の定理で仕上げです。

余弦定理で辺の長さを求めるときは二辺とその間の角が分かれば求められます。

また、三辺の長さが分かればcosの値を求めることができます。

この問題の場合は最初でフルに使います。

どちらかというと余弦定理の方が使いますし、役に立ちそうですね。

実は余弦定理は２つあって、今回証明したのは第2余弦定理と呼ばれるものです。

第2があれば第1があります。

でも第1余弦定理はあまり使いません。

使い勝手悪いですからね。

明日、どんなのかを解説します。

 

まとめると

正弦定理→1組の角とその対辺ともう１つの角か辺の長さがわかっている時

余弦定理(辺の長さ)→二辺とその間の角がわかっている時

余弦定理(cosの値)→三辺の長さがわかっている時

に使います。

今日の問題が練習になりそうですね。

明日は空間図形の問題ですが、そこでも使えます。

正弦定理と余弦定理は使いこなせるようになりたいところですね。